Machine Learning made easy!
Start training your own machine learning models today. You can use asanAI in any browser of your choice - and it is completely free to use!
This page offers a comprehensive overview on the theoretical foundations of asanAI.
When we talk about Data, three basic terms are especially important: vectors, matrices and tensors. Luckily, they are not as complicated as they seem. A vector is just an ordered set of numbers, like [1, 2, 3]. This vector has a length of 3. These numbers can be anything, they can be distances, prices, measured values and so on. If you take many vectors, you can build a matrix of them. If we agree that 1 is white and 0 is black, this gives us an image of the letter L. Color images, for example, are three such matrices, one for red, green and blue. You can imagine them as submatrices in a larger matrix.
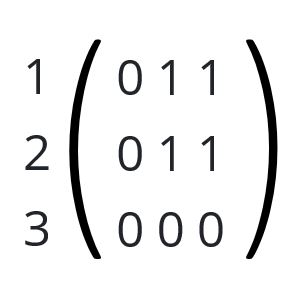
This is a so-called tensor. A tensor is a matrix that contains other matrices. The R, G and B Matrix have the same shape, 2 values wide and 4 values high. This is expressed as [2, 4]. The matrix around R, G and B is 3 values wide (each value a matrix) and 1 px height. The whole tensor then is [2, 4, 3]. These tensors can have any shape and any lengths. They can represent all kinds of data, no matter if they are images, sounds, videos, measured data and whatever else. If you can get it into a computer somehow, it can be represented as such tensors.
For a basic idea of what a neural network is, we need to take a look at functions. A function f(x) takes an input, does something to it and then outputs it again.
If we have x = 5, we get: 2 * 5 + 1 = 11. In neural networks, this is similiar, but the other way around. What we have is not the rule for the function, but it’s in- and outputs. For example, we may have a list like:
x, y
1, 3
2, 5
3, 7
4, 9
5, 11
6, 13
7, 15
8, 17
9, 19
10, 21
Now we tell the computer: This is an example of the input and output values to a function f(x) = y. Please find me a function that approximates this. Remember that X and Y may not only be numbers, but whole tensors with any number of dimensions, that also includes Images, Videos, complex measured data in science and so on.
One of the basic ideas is a neuron.
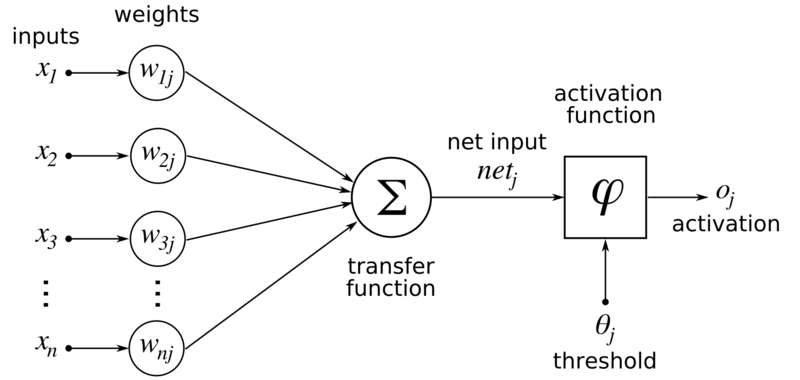
A neuron has many inputs. Ever input may be a number (or a tensor in more complex cases). Each of these inputs has a so-called weight. If the weight is 0.5 and the input number is 2, the neuron sees this input as 0.5 * 2 = 1. We may then also add a bias, which is just a number that is added after summation of all the weighted inputs.
The neuron simply sums up all of these inputs. This sum is then passed to an activation function. The function does something with the value, like squeeze it between 0 and 1 (where high values are closer to 1 than low ones). This is done to get nonlinearity in the network, so that it can detect more complex patterns than just linear ones.
When we have some neurons, we can group them into layers. The layers that contain only such neurons are called Dense Layers. One layer consists of one or multiple neurons. Within the layers, we do not connect these layers. But between the layers, we connect all of them with each one in the previous or next layer. The output of the last layer contains the results of our network.
A linear function, for example f(x) = 2x, would not need an activation function to get nonlinearity to approximate it. But nonlinear function, for example f(x) = tan(x) / sin(x), would need it. Question to decide whether you need an activation function: can a single line accurately represent my dataset or divide it into categories? If yes, activation function can be “linear” (same as no Activation function), otherwise you’d need an activation function. Another usage case for linear Activation would be that you want discrete large output numbers, like 19, instead of something between 0 and 1. Maybe then you need a linear activation in the last layer.
Some activation functions are specialized more than others. For Example, softmax will sum all the values that are given into it, and then return a percentage of how much these single values are from the whole.
SoftMax([1, 2, 5]) = [0.125, 0.25, 0.625].
Softmax’s Output always sums up to 1 (= 100%).
Internally, this is mostly just matrix (or tensor) multiplication and addition. The output is then another tensor (which may also be a vector or just a single number). This way, the whole neural network is a function.
The computer gets a list of values, called Training Data, so that it knows how the function should behave like. It takes some of those values (a “batch”) and gives it into the neural-network-function and sees what comes out. The output that should happen is known. Then the training algorithm looks at the difference in the outputs. This is called the loss. An example loss would be the Mean Absolute Difference (MAD). If the output vector should be [1, 2, 3], but the function gives us [2, 2.1, 4], the differences are [1, 0.1, 1], so the mean of this is (1 + 0.1 + 1)/3 = 0.7. So the loss (MAE) is 0.7. The function’s weights and biases are then corrected, so that the loss gets lower over time.
In classical algorithms, we have certainty of their results. If you implement it properly and the algorithm works, you always get correct results. But in neural networks, trade certainty for the ability to solve problems that we cannot solve otherwise. Neural networks rarely give exact results, but just good-enough approximations.
After training the network, you can predict new values. Predict means: get the outputs of the function with the potentially never seen input values. Imagine it on images: you’ve trained the network on 1000 images of dogs and 1000 images of cats to classify images into those 2 categories. If you give it an image it has never seen before (that was not in the training data) it should still be able to classify it correctly, even though the network has never seen the new data before.
